(今天连bluehost好慢
刚刚被虐回来,稍微总结一下
题的范围很广,从TCPIP协议、数据库、算法与数据结构、计算机系统到语言细节,都有涉及
另外今年的笔试题里有10道选择题、5道填空和加分题的第一题都与去年的题目一模一样 OTL……
没看去年的题亏死了
挑两道印象比较深的题记录下:
(都是去年的题,网上都有公开,应该不算是私自公布试卷了吧)
两人猜数字,范围为[1,100], 甲写一个数字,让乙猜。 如果乙猜的偏小,甲会说偏小,但是如果某一次甲猜的偏大,乙之后都只会说对或不对。 问: 乙最少可以在多少次内保证猜对?在这种策略下,第一个猜的数字是什么?
看到这道题,首先可以推导出这两问的答案一定是同一数字。若第一次猜X且偏大,则之后需猜X-1次方能保证猜中,即最少需猜X次。
于是递推一下,设最少猜X次才能保证猜对,则第一次必定猜X
第二次要猜多少呢?第二次猜的时候,要保证在猜偏大的情况下,后面再猜X-2次就能保证猜中,所以第二次要猜X+X-1
同理,第三次若猜偏大,后面要再猜X-3次,所以第三次猜的数为X+X-1+X-2……直至猜了N次之后,猜的数>=100
这就是一个初项为X,公差为-1,项数为N的等差数列求和,即约束方程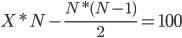 下求X的最小值
下求X的最小值
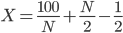 ,
,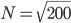 时有极值,X约为14
时有极值,X约为14
答案就是14 14
两个数组a[N],b[N],其中A[N]的各个元素值已知 现给b[i]赋值,b[i] = a[0]*a[1]*a[2]...*a[N-1]/a[i]; 要求: 1.不准用除法运算 2.除了循环计数值,a[N],b[N]外,不准再用其他任何变量(包括局部变量,全局变量等) 3.满足时间复杂度O(n),空间复杂度O(1)
在编程之美上出现过类似的
这个题不准用其他变量,那只能在a和b上下手了
我的思路是,对于b[i]来说,可以拆成a[0]*a[1]*...*a[i-1]和a[i+1]*a[i+2]*...*a[N-1]两部分,这两部分用O(n)分别求出来,最后再乘起来就行了
代码见下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | #include <stdio.h> void foo(int a[], int b[], int N){ b[0] = 1; //乘完左边,存在b[i]里。 此时b[i]表示从a[0] * ... *a[i-1]的积 for (int i = 1; i < N; ++i){ b[i] = b[i-1] * a[i-1]; } //乘完右边,存在a[i]里。a[i]表示从a[i] *...*a[N-1]的积 for (int i = N-2; i > 0; --i){ a[i] *= a[i + 1]; } //两边乘起来 for (int i = 0; i < N - 1; ++i){ b[i] *= a[i + 1]; } } int main(){ int a[10] = {1,2,3,4,5,6,7,8,9,10}; int b[10]; foo(a,b,10); for (int i = 0; i < 10; ++i){ printf("%d\n", b[i]); } } |
我这种写法的缺点是改变了输入数组a,这个不太好。把好写法贴一份:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | void problem(int* a, long long* b, int N) { b[0] = 1; for(int i = 1; i < N; ++i) { b[i] = b[i-1] * a[i-1]; // 分水岭的前半段乘积 } b[0] = a[N - 1]; for(int i = N - 2; i >= 1; --i) { b[i] *= b[0]; b[0] *= a[i]; // 分水岭的后半段乘积,是从数组尾部向前循环的 } } |
一条评论
还是成都站的要简单些