这回是自己偷偷把试题带回来了。这次比赛一共就一道题,上午9点做到晚上5点,不能上网,中午管饭
之前听说往届都有界面需求,这机房只有vc6,所以前几天还补了下mfc,果然太难用了……
今天一看题目,不需要界面,还好还好
不过也是做得异常地郁闷,真是费劲千辛万苦最后才搞出一个不怎么靠谱的答案,对比赛成绩不能有任何的指望了,就当是蹭饭机房一日游
题目是这样的:
=======================================================================
编程题(共1题,100分。请上机编写程序,按题目要求提交文件。测试用例不对考生公开,凡不满足提交要求导致不能运行或用例不通过,不予评分。)
1. 俄罗斯方块之棋盘覆盖
俄罗斯方块是一款风靡全球的益智类游戏。由俄罗斯人阿列克谢·帕基特诺夫发明,故得此名。俄罗斯方块的基本规则是移动、旋转和摆放游戏自动输出的各种方块,使之排列成完整的一行或多行并且消除得分。由于上手简单、老少皆宜,从而家喻户晓,风靡世界。
本试题是在俄罗斯方块几种常见的方块基础上,在指定大小和障碍的棋盘上,用标准的方块形状,完成对棋盘的覆盖。用于覆盖棋盘的方块可以是下文所给出方块的全集,也可以是其中的任意一个子集,且使用的方块数量不限,形状变化不限。
棋盘大小:
棋盘大小为21行21列的正方形。按照从上到下,从左到右,从1开始,依次进行编号,直到最右下方的格子标识为441。
可选方块:
可选方块为标准的俄罗斯方块形状,包括其标准的旋转变化。基本形状如图所示:
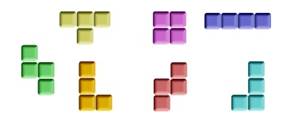
各形状的变化如图所示(字母为方块编号):

障碍说明:
棋盘上仅有一处障碍无法放置方块,障碍可处于棋盘任意位置。障碍为基本形状a及其所有的旋转变化,如图所示:
输入输出要求:
输入文件名为testin.txt,格式如下所示,各数字用空格隔开,各数字表示棋盘格子编号。
2 3 22 23
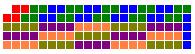
输出文件名为testout.txt,要求先输出棋盘覆盖结果,再输出未覆盖的格子个数。输出棋盘用21行21列数字/字母表示,其中0表示未覆盖的格子,1表示障碍,字母表示对应方块编号(字母对应关系见“可选方块”一节)。最后输出未覆盖格子个数。这里以6行10列棋盘举例示意输出格式(注意:实际输出应该是21行21列,对应方块形状用对应的字母表示):
要求:
1、 用所提供的方块尽可能覆盖棋盘并输出结果;
2、 在(1)的基础上,棋盘上的空格越少越好。
交付件要求:
C/C++:需要提交可执行文件和压缩打包的源代码工程
JAVA:需要提交压缩打包的整个编码工程目录
==============================================================
点此直接跳到最后的构造法及代码
一看题目,第一感觉是搜索空间有点大,第二感觉是说不定旋转对称性可以利用,不管了先给他搜上再说
慢吞吞地写完后,一运行,╮(╯_╰)╭ ………………加了记忆也没用
然后开始使用无脑流乱改,眼瞅着那个长条挺好用,给我把大片的空白全填了去!
填到只剩6行(考虑到unsigned long 是128位,6 * 21 =126正好小于128就留了6行),还是特别龟速
然后稍微注意了一下,用我的土算法,实际搜索范围在7x7的时候就很慢了,再往上肯定无理
所以要么换搜索算法,要么就把搜索范围进一步缩小。
之前产生用长条填的想法,是基于以前看的俄罗斯方块视频。那位神玩家基本可以在任何情况下都使用长条一次性消去三四行,所以我觉得这道题可以整行整行地填充以缩小搜索范围,而不至于太过影响最终结果。看来光是按行填还不够
算法方面暂时想不出什么办法了,我需要一个好的启发式搜索剪枝算法!但是想不出……先吃饭嗯。这黄瓜好辣
吃完饭,想想觉得有个不怎么靠谱的结果总比一万年也跑不出个结果要强,于是把原来的算法改成不可靠算法,遍历的次序随机化,也只按照一定概率进行回溯。这下结果总算是有了,还可以跑个几百次取最佳值,最佳结果一般在9到20之间浮动。我在想,一共21行,这样的话就是每行不超过一个空,这电脑已经能玩的比我还好了。但是毕竟是比赛口牙,时间也还有,就再努努力试试
于是视线重回搜索范围,在长条填充的想法上进一步深入,填到只剩一个很小的方形如何?毕竟之前测试发现小范围搜索下遗留的空位也都很少
先看地图大小,21x21,长条填充的话是4+4+4+4+4+1(竖着),所以要想填充完整,这个方形的尺寸只能是4的倍数或4的倍数+1
考虑到之前的7x7最大值,我选择5x5的方形尺寸。21-5=16,这样只要保证这个方形两边的余下的长度都能被4整除,就可以用长条完美覆盖了
而障碍物的尺寸是2x3,长度为2的那条边肯定能被起始位置为4的倍数、尺寸为5的方形装入。而长度为3的那条边讨论起来就有点麻烦了
稍微画了下图,发现用障碍物的左上角位置对4取模,余数为0、1、2都没问题,3的话就只有增加方形尺寸。于是在这种情况下,把方形尺寸加到8,依旧可以较为完整地用长条铺满,只不过需要补一个长条,损失一个无法填补的位置。5x8也小于7x7,性能也可以接受。
之后做了下实验,5x5的小方形里会留1个空,5x8的小方形里不会留空,但是5x8时外面填充会有一个空,这样两处加起来也正好是1个空,比之前的随机算法效果好多了
不过依旧是不完美算法OTL ,不知道该怎么证明子空间的最优性。再说满眼都是 f 这算什么嘛!也完全不能保证找到最优解。最优解我是无论如何也想不出的,只能再多查找资料、多积累了。
后记:
和罗同学讨论、阅读了宝贵的博客留言后,思路也稍微明晰一点了。首先21x21,最优解为遗留1个空,这个我就完全没有察觉到……太沉浸在性能测试上了,性能测试时使用的棋盘大小又不是21x21的
晚上回来重新debug,发现自己的算法还是勉强可以完成只遗留1个空的(通过枚举小方形,但依旧不知道怎么证明),但是比赛时提交的代码里有错误,横向的情况被我写反了(左右颠倒了OTL 都没有认真核对障碍的形状就交上去了),这样一来一半的测试用例肯定都通不过了
我的实力也就仅此而已了,愿这次的失败能让我沉淀得更深
============================================================================
这两天也和网友进行了讨论,还是构造法最高啊……
构造法说起来也很简单,首先利用对称性和可旋转性,将输入缩减为一种(这里都缩减为![]() ),之后对输入的位置进行考虑:
),之后对输入的位置进行考虑:
若位于左上角,则可以通过如下的方式填充:
剩余的空格就是左上的第一个格子,剩下的21x16区域用长条可以完美填充
(右下角也是完全一样)
若不位于左上角或右下角,则可通过加入两个L,变成![]() 或
或![]() 的4x3的障碍。将障碍体积变为4x3后,剩下的区域再用长条填充,可以保证填充至只剩1个格子(简单画画图就能发现了,不证明了)。
的4x3的障碍。将障碍体积变为4x3后,剩下的区域再用长条填充,可以保证填充至只剩1个格子(简单画画图就能发现了,不证明了)。
被别人一点拨,感觉真的是醍醐灌顶,如此简易的分析方法自己便就是做不到口牙……!
照着这个思路,自己也大致写了下代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 | #include <stdio.h> #include <stdlib.h> #include <memory.h> #define TABLE_SIZE 21 // store the input int input[4] = {0}; // store the hole answer char table[TABLE_SIZE * TABLE_SIZE]; bool isVertical = false; void Initialize(); void Output(FILE* f); void Construct(); int main(){ FILE* fw = fopen("testout.txt", "w"); FILE* fp = fopen("testin.txt", "r"); if (!fp){ printf("file not found!\n"); return 0; } // main loop while (!feof(fp)){ fscanf(fp, "%d %d %d %d", &input[0], &input[1], &input[2], &input[3]); Initialize(); Construct(); Output(fw); } fclose(fp); fclose(fw); return 0; } void Initialize(){ int i, j, x, y; memset(table, 'f', sizeof(table)); for (i = 0; i < 4; ++i){ if (input[i] < 1 || input[i] > TABLE_SIZE * TABLE_SIZE){ printf("input number error!\n"); exit(0); } --input[i]; // input pos start from 1... but I start from 0 } //sort input for (i = 1; i < 4; ++i){ if (input[i] < input[i - 1]){ int temp = input[i]; for (j = i - 1; j >= 0 && input[j] > temp; --j){ input[j + 1] = input[j]; } input[j + 1] = temp; } } //rotate input to 3x2 if it is 2x3 if (input[1] - input[0] != 1){ isVertical = true; for (i = 0; i < 4; ++i){ x = input[i] % TABLE_SIZE; y = input[i] / TABLE_SIZE; input[i] = x * TABLE_SIZE + TABLE_SIZE - 1 - y; } input[0] ^= input[1]; input[1] ^= input[0]; input[0] ^= input[1]; } } void Construct(){ int i, j, x, y; x = input[0] % TABLE_SIZE; y = input[0] / TABLE_SIZE; if (input[0] == 1 || input[0] == TABLE_SIZE * TABLE_SIZE - 2 - TABLE_SIZE){ // in the corner (left-top or right-bottom) if (input[0] == 1){ table[0] = '0'; }else{ table[TABLE_SIZE * TABLE_SIZE - 1] = '0'; } for (i = 1; i < TABLE_SIZE; ++i){ table[i + y * TABLE_SIZE] = 'a'; table[i - 1 + (y + 1) * TABLE_SIZE] = 'a'; } }else{ //fill it with L in a 4x3 tiny block (3x4 is also useful) if (y != TABLE_SIZE - 2 && x != 1){ for (i = x - 2; i < x + 2; ++i){ for (j = y; j < y + 3; ++j){ table[i + j * TABLE_SIZE] = 'c'; } } }else{ for (i = x - 1; i < x + 3; ++i){ for (j = y - 1; j < y + 2; ++j){ table[i + j * TABLE_SIZE] = 'c'; } } } //leave a hole anywhere if (table[0] == 'f'){ table[0] = '0'; }else{ table[TABLE_SIZE - 1] = '0'; } } // fill the barrier for (i = 0; i < 4; ++i){ table[input[i]] = '1'; } } void Output(FILE* fp){ int i, j; for (i = 0; i < TABLE_SIZE; ++i){ for (j = 0; j < TABLE_SIZE; ++j){ if (isVertical){ fprintf(fp, "%c ", table[TABLE_SIZE - 1 - i + j * TABLE_SIZE]); }else{ fprintf(fp, "%c ", table[i * TABLE_SIZE + j]); } } fprintf(fp, "\n"); } fprintf(fp, "1\n"); } |

12 条评论
2 3 22 23什么意思?
表示在第2、第3、第22、第23这4个位置有障碍,如果以21x21大小的棋盘左上角为1,先横着数再竖着数,则这4个位置正好构成图中所示的那个俄罗斯方块图案
顶一个!!!
棋盘共有441个格子,每个现状都是4格,441%4 = 1;剩下的空格数只可能是1,5,9,13.。。
直接暴力求解,每种障碍都能算出剩一个空格的布局。已经是最优的了
感谢提醒,但是直接暴搜好像很慢啊,110个图案填进去的组合数太多了。如果先缩小区域再暴搜,主要的障碍是对小区域内能达成最优(即剩1或0个格子)的证明。这个证明只能靠枚举么?
有同学做了,对任何位置的障碍都能填充到只剩一个空格(本来至少会留一个空格 )。先和你得做法一样对4的倍数的行(不包含障碍的行)用f填满,缩小范围。这时其实在下面用笔分析出了只剩一个空格的填充法,没有在程序里搜,程序里面只是一些赋值。。。只要做出一种障碍,另外一种障碍旋转得到第一种障碍,再解决就行了。。
我做出来的结果都是5,如果要求都是1的话,程序要更复杂,没时间写了。
其实我想知道有多少人是构造的。。。。。
而且其实构造的时候有个小trick,有一个情况下构造3*4(对于您这种情况,我的情况是4*3)的方块的时候,会把那个空白覆盖掉。我是写了一个check才发现的。没有太多时间看您的程序,不知道是否有相似的问题。
抱歉……稍微有些没看懂您的意思
文后那份代码里,在确定了构造4x3 / 3x4的矩形之后,其他地方就全用长条填充,再随意留一个空就可以了。只要先确定矩形位置,再确定留空的位置,就不会让空隙被覆盖了。
我的填充方法跟你略有差异。
- -表示当时直接用excel画了一下,于是。。。我还在压缩包里加了个excel文件。。。
这题比前两届的简单多了,不知道华为最后怎么评判。。。
我边拿笔算边看题目,我想到的是将其障碍变成4x3的障碍,就如你所说的4x3的障碍。可是就没想到剩下的分配了...哈哈。自己也忍不住往下看你的做法,就没再想直接跳到你的算法中。
dsd